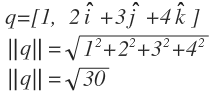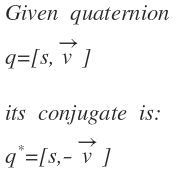Introduction

While crossing a bridge with his wife, Sir William Hamilton made a mathematical discovery so profound he carved it onto a stone. After 10 years of work, he had finally found a way to simultaneously rotate about multiple axis. He named his discovery Quaternions.

Although his discovery went unnoticed for a while, it wasn't until the flight simulation and computer graphics industry that Quaternions mathematics became alive again. Quaternions are mainly used in computer graphics when a 3D character rotation is involved. Quaternions allows a character to rotate about multiple axis simultaneously, instead of sequentially as matrix rotation allows. For example, to rotate 45 degrees about the xy-axis using matrix rotations, the character must first rotate about the x-axis and then rotate about the y-axis. With quaternions this sequential process is not necessary.

Why use Quaternions to rotate a 3D character when matrices can do the same job? There are two reasons why Quaternions are preferred in computer graphics:

1. Matrix rotations suffer from what is known as Gimbal Lock.
2. Quaternions consume less memory and are faster to compute than matrices.

Gimbal lock is the loss of one degree of freedom in a three-dimensional, three-gimbal mechanism that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space. 2

The goal to talk about quaternions is to see how they can help us rotate characters more efficiently. However, before we talk about rotations, let's learn a bit more about quaterion arithmetics. .

Quaternions

Quaternions are composed of a scalar and a vector. They are represented in various different ways such as:

where S is a scalar number and V is a vector representing an axis.

Adding and Subtracting

Quaternions can be added and subtracted among themselves. In quaternion addition and subtraction, the corresponding scalar and vectors from each quaternion are added/subtracted, respectively. Mathematically, quaternion addition/subtraction is represented as follows:

For example, the addition of two quaternions is calculated as follows:

Product

Quaternions can be multiplied among themselves. Mathematically, quaternion multiplication is represented as follows:

Scalar Multiplication

Just like vectors and matrices, a quaternion can be multiplied by a scalar. Mathematically, this is represented as follows:

where k is a scalar real number.

Square

The square of a quaternion is given by

For example, the square of quaternion q is calculated as follows:

Norm

Mathematically, the norm of a quaternion is represented as follows:

For example, the norm of quaterion q is calcuated as follows:

Unit Norm

The unit norm of a quaternion, also known as Normalised quaternion, is calculated as follows:

For example, normalizing the quaternion q is calculated as follows:

Conjugate

The conjugate of a quaternion is very important in computing the inverse of a quaternion. Mathematically, the conjugate of quaternion q is calculated as follows:

Inverse

The ability to divide in quaternion arithmetic is very important. To be able to divide a quaternion, you need its inverse. By definition the inverse quaternion satisfies the following:

The inverse of a quaternion is defined as:

Reference: Quaternions for Computer Graphics by John Vince